Blog

It is obvious that Warcaster has a unique dice system, but not so obvious how big an effect this can have. In particular, there is a lot more potential for ‘swingy’ extreme damage than other games. Due to the opposed rolling system, any model can roll high at the same time the defender rolls low, and chains of super strikes can crank the numbers high.

Basics of dice

I can go into a detailed analysis of how various dice work: but Privateer Press already did a great comparison of D6, 2D6 and Strike Dice systems. I’ll put this here and wait for you to return

Strike Dice 101

Ok, welcome back. Key differences

• D6 is equally likely through the range, the outcome of an individual roll is unpredictable, and the impact of buffs is the same throughout the range
• 2D6 (and 3D6, 4D6…) forms a normal distribution with 7 being most likely, and most (66%) of results around 5-9. A better attacker will need a lower number to beat in the range of 2-12. Adding 2 to a roll has a lot more impact if it moves from an 8 to a 6, compared to other areas, and in most cases a better attacker or defender shift what dice are needed.
• Strike Dice skew the distribution, with a ‘long tail’ of unlikely but possible results as more dice are rolled. A single white die will roll on average 0.666 and a red die will roll 1, however both can roll a maximum of 2 (1/6 chance).

In Warcaster, a stronger attacker gets to roll more dice to reach higher numbers, and the opposed rolls let the defender deduct their result from the attacker’s. Unlike most systems where rolls are independent, in Warcaster the ‘hit’ roll adds more red dice to the damage roll (expected value 1 damage strike). Some impacts

• An attacker with more RAT or MAT can roll a lot more dice, making it more likely they hit AND carrying each additional strike into the damage roll. This tends to make RAT / MAT and additional dice on the Hit roll more valuable than Weapon POW.
• The contested dice system for hitting: on average the rolls of the attacker and defender cancel out, however it allows for extreme outcomes where the attacker rolls high and the defender rolls low. Effectively there are 2 chances for randomness, and they can add together.
• It also means rolling a really strong attack roll (or an opponent’s really bad defence roll) can snowball into ridiculously high damage.

Scenarios

So looking at the implications for 3 scenarios, based on the power balance between attacker and defender. The way to analyse probabilities is different for each

• Evenly matched attacker and defender, where you’d expect to damage but not destroy them (Firebrand shooting marauder with his assault rifle)
• A powerful attacker expected to easily kill the target (Divine Tempest swords against a paladin enforcer)
• A weak attack, expected to do nothing (Paladin Enforcer shooting a Scourge warjack)

In all cases we are assuming the attacker is charged, and I am using Arcane Stats to analyse the probability.

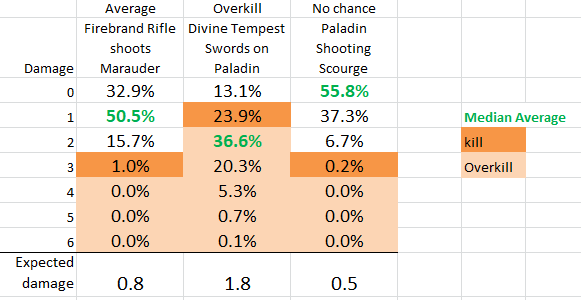
I’ve put it in excel to add some notation – and show 2 forms of average.

• Median: the 50th percentile: calculated by counting up the cumulative damage until you hit the “50%” bin and shown in bold green. This is a fair expectation from a single damage roll, and there is equal probability of being above and below it.
• Mean / Expected damage: This includes a decimal point, but is what you’d expect on average over many rolls. 0.8 damage doesn’t make too much sense from 1 roll, but if you took this shot 10 times you’d expect to have done 8 damage. This includes extreme results better than the median, but gives a similar number in the scenarios above.

Evenly matched: average 1 damage

In this case, a decently powerful attack is hitting someone who can take it: the average damage will hurt but not destroy the marauder.

• The average damage is about 1. There should be equal probability of being above or below this result, although this example doesn’t show this because the 1 result is so wide (50% of the total range).
• Poor dice will do 0 damage about 1/3 of the time, and a high result ~1/6 of the time does 2 damage. There is also a 1% chance to destroy the marauder in 1 hit.
• Because there is a chance to be below and above, the median and expected are both reasonable guides for what you’d expect, and over 3-4 attacks (which my Firebrand has) you should destroy he Marauder on average.

Overkill target: 87% of the time it works every time

In this scenario, the Divine Tempest’s high intensity swords should be easily able to kill the Paladin, with the average (P50) at 2 damage against the paladin’s single health.

• It is possible to roll higher but at this point you are not talking about damage, just arguing over how small the pieces are.
• The only meaningful variation is on the low side, where there is a 13% chance to do 0 damage.
• This quickly reduces the entirety of the curve to a single probability: 13% chance to do nothing, 87% chance to kill the paladin outright.

While the Divine Tempest is an extreme attacker, all attacks on single wound infantry reduce to this binary outcome, just with various probabilities of killing them or not. In all cases, the average damage is less important than the probability of killing (by doing 1 damage).

Paladin shooting Scourge – EXTREME DAMAGE!

In this example, noone thinks a single rifle shot has any chance to harm the scourge. More than likely (P50) it will do 0 damage.

But roll enough dice, add a charge, and there is a 0.2% chance of destroying it. While incredibly unlikely, it is possible to roll 2 strikes on every die. If this combines with the defender rolling 0, you can carry a lot over to the damage roll. Once you have a huge number of dice in the damage roll, anything can happen.

This is an extreme example, but even without these dice, a squad of paladins have a pretty good chance to kill a light warjack. Firstly there are 3 chances to get the 0.2% instant kill shot. But almost half of attacks roll at least 1 damage, and occasionally (~7%) one will roll 2 damage.

Looking at the probabilities in ArcaneStats: with 3 charged rifle attacks there is a 20% chance to kill outright, 50% chance to do 2 damage, and 80% chance to do at least 1. If you add their potential bayonet attacks, the probability to kill increases to 55%

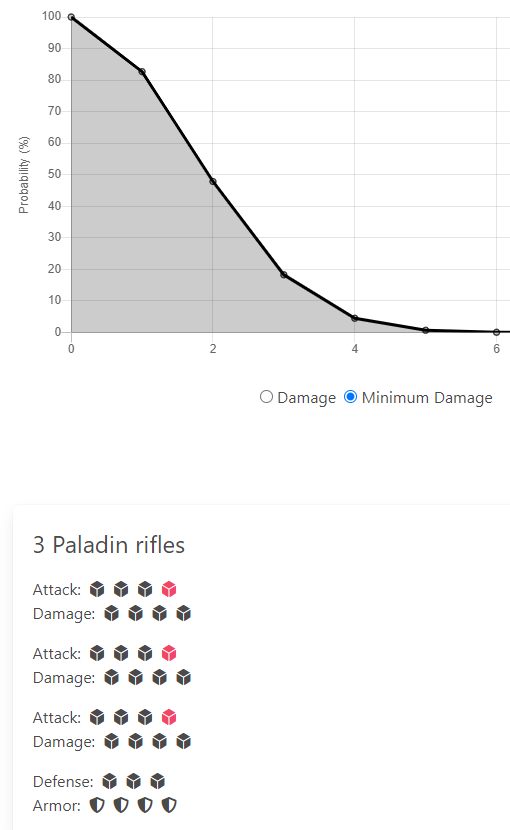
The ability for the attacker rolling high at the same time as defender rolls low can give very large damage swings in Warcaster – basically anything can kill anything on a good day. If you really need to kill something, it can’t hurt to take a few shots with whatever you have on hand.

Conclusion

We’ve talked through the probability system, tested some scenarios using ArcaneStats, and given 3 examples with different ways to analyse probability

1. In an evenly matched scenario, P50 (median) is a reasonable guide to expected output from a roll, although it is possible to do nothing and probably possible to kill the target.
2. Against a single wound target, you’re usually more interested in the probability to kill % rather than the expected damage
3. If you have no right to do any damage, the expected output might give you an idea of how many attacks are needed to do anything. And even if you don’t have enough attacks, there is often a chance to do some damage anyway.

Finally, be aware that this is a very unpredictable game, and almost anything can kill anything else if the dice are on your side. This can often favour aggressive play: destroy or stun (cryo lock) what you can before it hits you, because there’s no guarantees of surviving even if you try to hide away from the action.